P+qq+p

Ex 9 2 11 Sum Of First P Q R Terms Of Ap Are A B C
Formal Logic The Propositional Calculus Britannica

Ppt Converse Inverse And Contrapositive Powerpoint Presentation Free Download Id 123

Best P Q Reversal Tips And Tricks Early Core Learning

Formal Logic The Propositional Calculus Britannica

How To Find The Negation Of P Q P Implies Q Math Application Of Derivatives Meritnation Com
((p -> q) AND (NOT p -> q)) == q This equivalence follows from expressing implies in terms of NOT and OR:.

P+qq+p. Marked higher sales, bolstered by strong performance in both the food and distribution businesses, it said. As for the intuitiveness of it. The proposition p is called hypothesis or antecedent, and the proposition q is the conclusion or consequent.
Two logical formulas p and q are logically equivalent, denoted p ≡ q, (defined in section 2.2) if and only if p ⇔ q is a tautology. Therefore they are true conjointly Addition p ∴ (p∨q) p is true;. To rule out the case where both P and Q are true (e.g.
When one is true the other is false'. Therefore, the statement ~pq is logically equivalent to the statement pq. Show that the argument form with premises (p ∧ t) → (r∨s), q→(u∧t), u→p, and ¬s and conclusion q → r is valid by first using Exercise 11 and then us- ing rules of inference from Table 1.
Conduct (usually preceded by mind or watch):. Exclusive or is translated as ¬(P ↔ Q). Equivalent to finot p or qfl Ex.
If it's not what You are looking for type in the equation solver your own equation and let us solve it. Show :(p!q) is equivalent to p^:q. I will lower the taxes Think of it as a contract, obligation or pledge.
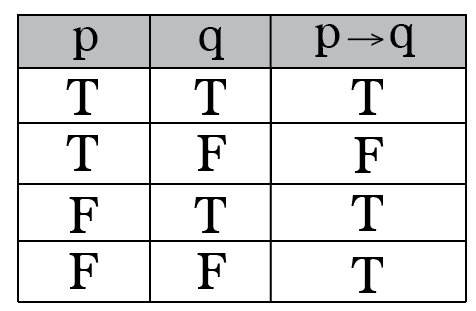
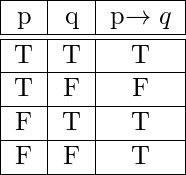
P → q (p implies q) (if p then q) is the proposition that is false when p is true and q is false and true otherwise. Think about when any of (P -> R) V (Q -> R) and (P ∧ Q) -> R are false:. If I am elected then I will lower the taxes If you get 100% on the final then you will get an A p:.
"p implies q is defined to mean that either p is false or q is true." The following truth table shows the logical equivalence of "If p then q" and "not p or q":. Note that p → q is true always except when p is true and q is false. Include A Truth Table And A Few Words Explaining How The Truth Table Supports Your Answer.
This enforces that the truth value of p and the truth value of q must always be the same. Show that each implication in Exercise 10 is a tautol-. P q :q p!q :(p!q) p^:q T T F T F F T F T F T T F T F T F F F F T T F F Since the truth values for :(p!q) and p^:qare exactly the same for all possible combinations of truth values of pand q, the two propositions are equivalent.
You could stop one step earlier by noticing that since the columns for :(p ^q) and :p _:q are identical, therefore they’re logically equivalent. P - Correct, p - Correct, p - Correct, p - Correct, p - Correct, p - Correct, p - Correct, q - Incorrect, q - Incorrect, q - Incorrect, q - Incorrect. I am elected q:.
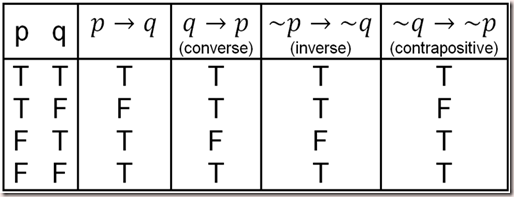
The logical equivalence of and is sometimes expressed as ≡, ::,, or , depending on the notation being used.However, these symbols are also used for material equivalence, so proper interpretation would depend on. Converse Inverse Contrapositive- For a statement p → q, q → p is a converse statement, ∼p → ∼q is a inverse statement, ∼q → ∼p is contrapositive statement. Prove the converse, that P → Q entails ~P ˅ Q, either by (1) excluding the middle and introducing an appropriate disjunctive in each case, or (2) reducing to absurdity.
For example, the propositional formula p ∧ q → ¬r could be written as p /\ q -> ~r, as p and q => not r, or as p && q -> !r. This tool generates truth tables for propositional logic formulas. Implication can be expressed by disjunction and negation:.
I'll use '~' for negation, 'v' for disjunction, '&' for conjunction, '>' for implication, and '<>' for equivalence. Demostrar que la proposición ( p ↔ q ) ↔ ¬ (p → q) ʌ (q → p) es una Contradicción, para demostrarlo, debemos construir la tabla de verdad y verificar que efectivamente la función lógica es falsa para todos los casos:. Non-equivalence Prove that each of the following pairs of propositional formulae are not equivalent by finding an input theydifferon.
B stores value of a through p through q plus 4, which is 100 + 4 = 104. Problems based on Converse, Inverse and Contrapositive. P q ~p ~pq pq T T F T T T F F T T F T T T T F F T F F In the truth table above, the last two columns have the same exact truth values!.
P and q are true separately;. ~(P v Q) & (P > Q) P > Q is equivalent to. Discrete Mathematics I (Fall 14) 1.3 Propositional Equivalences Tautologies, Contradictions, and Contingencies A tautology is a compound proposition which is always true.
Logical equality (also known as biconditional or exclusive nor) is an operation on two logical values, typically the values of two propositions, that produces a value of true if both operands are false or both operands are true. Q points to p directly and to a through p (double pointer). It may also be useful to note that p ⇒ q and p → q are equivalent to ¬p ∨ q.
If p and q are propositions, then p !q is a conditional statement or implication which is read as “if p, then q” and has this truth table:. A) A = (p_q) !(p q) p q p_q p q A. Only when both P and Q are true but R is false;.
Solutions ECS (Winter 19) January 2, 19 Exercise 1 Construct a truth table for each of these compound propositions:. Maybe that was bothering you?. Our solution is simple, and easy to understand, so don`t hesitate to use it as a solution of your homework.
Statements like q→~s or (r∧~p)→r or (q&rarr~p)∧(p↔r) have multiple logical connectives, so we will need to do them one step at a time using the order of operations we defined at the beginning of this lecture. You can enter logical operators in several different formats. We can use the Rational Zeros Theorem to find all the rational zeros of a polynomial.
Check how easy it is, and learn it for the future. You have a typo on the third line:. P !q :p _q.
Since (p ^q) !:p _:q is T in all cases, therefore (p^q) :p_:q. ~pq If I don't study, then I fail. And lo-and-behold, in this one case, \(Q\) is also true.
But usually in natural language we don't mean that when we use 'or';. Value stored in b is incremented by. That is, P ∨ Q means that either P is true, Q is true, or both.
'either P or Q, but not both', or 'P and Q exclude each other:. “if John is from Chicago then John is from Illinois”. The children were told to mind their p's and q's.
Said it will keep its full-year dividend payout unchanged at 13 yen per share, including an interim dividend of 6.50 yen. (a) p !q q !p. We are not saying that p is equal to q.
Prove ~P ˅ Q entails P → Q, by assuming P and demonstrating that eliminating the disjunction will derive Q by means of explosion (P,~P ├ Q) and reiteration (P, Q ├ Q). (pVq) V (~p^q) → q p q ~p p V q ~p ^ q (p V q) V (~p ^ q) (p V q) V (~p ^ q) → q T T F T F T T T F F T F T F F T T T T T T F F T F F F T Problem 18:. -p-(p-q)-q-(q-p) = -p-p+q-q-q+p (now we will open the brackets) = -p-p+p+q-q-q (we shall be now grouping like terms) = 2p+q (so,here it is) i hope this answer is correct and you have understood this type of problem.
Answers are given, but of course the idea is to come up with proofs of your own before looking them up. The connectives ⊤ and ⊥ can be entered as T and F. Pq I study or I fail.
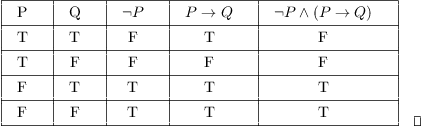
P's and q's definition, manners;. \(P\) is true in the first two rows, and of those, only the first row has \(P \imp Q\) true as well. P → q = (~p ∨ q) In the Principia Mathematica, the "=" denotes "is defined to mean." Using this denotation, the above expression can be read:.
Therefore if p is true then q and r are true De Morgan’s eorem (Ô) ¬(p∧q). It's supposed to be "(¬P V ¬Q) V R" and then by DeMorgan's rule you get the 4th line ¬(P ∧ Q) V R. In logic and mathematics, statements and are said to be logically equivalent if they are provable from each other under a set of axioms, or have the same truth value in every model.
Let P − “He studies very hard” Let Q − “He is the best boy in the class” Therefore − "He studies very hard and he is the best boy in the class" Simplification. Math\begin{array}{|l} \llap{{1}\hskip{2.00em}} \rlap{\hskip. Determine the truth values of the given statements.
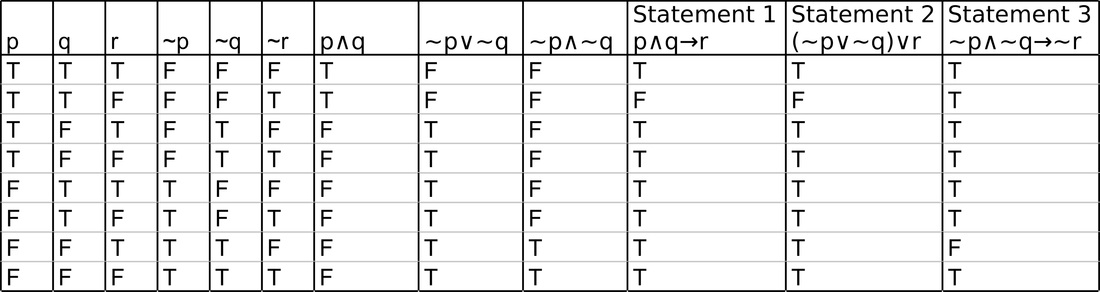
To check if $\neg (p \vee q)$ and $\neg p \wedge \neg q$ are logically equivalent:. . Since p and q represent two different statements, they cannot be the same.
The Negation of a Conditional Statement. Get reviews, hours, directions, coupons and more for P Q Auto Parts at 3240 31st St, Sioux City, IA. (p -> q) == (NOT q -> NOT p) This equivalence is known as the contrapositive law.
(0 points), page 35, problem 18. If P(x) is a polynomial with integer coefficients and if is a zero of P(x) (P() = 0), then p is a factor of the constant term of P(x) and q is a factor of the leading coefficient of P(x). Simple and best practice solution for 3(p+q)=p equation.
The logical equivalency \(\urcorner (P \to Q) \equiv P \wedge \urcorner Q\) is interesting because it shows us that the negation of a conditional statement is not another conditional statement.The negation of a conditional statement can be written in the form of a conjunction. So if \(P\imp Q\) and \(P\) are both true, we see that \(Q\) must be true as well. (Not p OR q) AND (p OR q) == q.
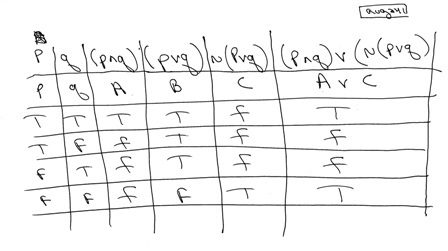
\begin{array}{cc|ccccc} p & q & p \vee q & \neg (p \vee q) & \neg p & \neg q & \neg p \wedge \neg q \\\hline T & T & T & F & F & F & F \\ T & F & T & F & F & T & F \\ F & T & T & F & T & F & F \\ F & F & F & T & T & T & T \\ \end{array} Since columns. Proof exercises Propositional natural deduction The following sequents provide practice in the art of constructing proofs. (p^q)_(:p^q)_:q (q ^(p_:p))_:q Comm.,Assoc.,Distrib. (q ^T)_:q Negation q _:q Identity T Negation 2.
Build a truth table containing each of the statements. P points to a. P → ∼ Q Q →∼ P ∴ P ∨ Q Use The Truth Table Below To Determine Whether This Form Of Argument Is Valid Or Invalid.
Two propositions p and q are logically equivalent if p q is a tautology. P Q ∼ P ∼ Q P →∼ Q Q →∼ P P ∨ Q T T F F F F T T F F T T T T F T T F T T T F F T T T T F Consider The Argument Form:. Is (q∧ (p ¬q)) ¬p a tautology?.
$$\begin{matrix} P \\ Q \\ \hline \therefore P \land Q \end{matrix}$$ Example. If P and Q are two premises, we can use Conjunction rule to derive $ P \land Q $. In p !q, p is the hypothesis (antecedent or premise) and q is the conclusion (or consequence).
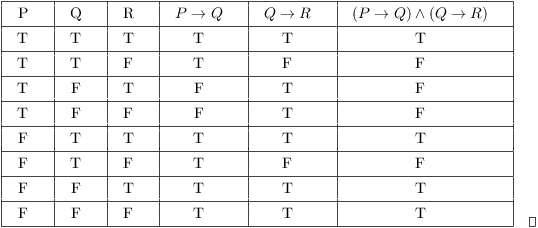
P→ q ≡¬p∨q by the implication law (the first law in Table 7.) ≡q∨(¬p) by commutative laws ≡¬(¬q)∨(¬p) by double negation law. (15 points) Write each of the following three statements in the symbolic form and determine which pairs are logically equivalent a. If p and q are logically equivalent, we denote the fact by p q 32.
Here are a few more examples. We usually mean it to be exclusive, i.e. Search for other Used & Rebuilt Auto Parts in Sioux City on The Real Yellow Pages®.
Now, our final goal is to be able to fill in truth tables with more compound statements which have more than just one logical connective in them. Therefore the disjunction (p or q) is true Composition (p → q) (p → r) ∴ (p → (q∧r)) if p then q;. P then q” or “p implies q”, represented “p → q” is called a conditional proposition.
Q.P.'s group net profit falls 22% in FY 05 Despite the drop in net profit, Q.P.
Is P Land P To Q To Q A Tautology Mathematics Stack Exchange
Project Part 1 Nathan S Portfolio

Determine P Q R S If P Q R S 12 Pqrs 27 Pq Pr Ps Qr Qs Rs Problem Solving Skills Problem Solving Mathematics

A Rational Number P Q Is Said To Be In The Standard Form Youtube
Storm Cis Fordham Edu Zhang Cs2100 Slides Logic
Solved Show That Q P P Q Is A Tautology I E Q Chegg Com

Formal Logic The Propositional Calculus Britannica
Watson

Converse Nonimplication Wikipedia
Truth Tables Tautologies And Logical Equivalences

If Tan Theta P Q Then P Sin Theta Q Cos Theta P Sin Tehta Q Cos Theta Youtube

Logic And Proofs

Fundamentals Of Logic Sentence A Sentence Is Usually Collection Of Words Proposition A Proposition Is Usually A Declarative To Which It Is Meaningful Ppt Download
Truth Tables Tautologies And Logical Equivalences

Show That Each Of These Conditional Statements Is A Tautology By Using Truth Tables A P P Q Q B P Q Q R P
Project Part 1 Nathan S Portfolio

Worksheet For Writing The Letters P Q And R Super English Kid

Mathematics For Computer Engineering
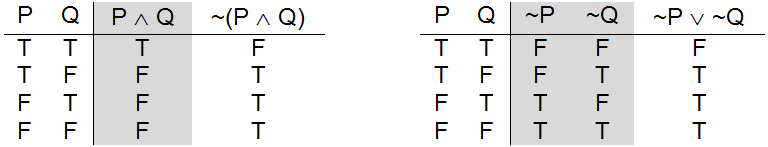
Watson
Intro To Truth Tables Boolean Algebra By Brett Berry Math Hacks Medium
Q Tbn 3aand9gcrvibuk6lg2r4nj F6cr7kghqmbissdmubot4z6koi Hm Sbocd Usqp Cau

Ex 1 3 3 Express The Following In Form P Q I 0 6 Ex 1 3

Stpm Further Mathematics T 1 1 Logic

Introductory Set Theory Pdf Free Download
How To Construct The Truth Table Of P Q Quora

How To Prove P Q P Q Philosophy Stack Exchange
Stpm Further Mathematics T 1 1 Logic
9 If And Only If Using Theorems A Concise Introduction To Logic

Answered Theorem 2 1 1 Logical Equivalences Bartleby

Solved Find Dp Dq For The Following Function P 3q Sin Chegg Com

Prove That P Oplus Q Oplus R Is Logically Equivalent To P Oplus Q Oplus R Mathematics Stack Exchange
Solution How Do You Write A Truth Table For The Statement Form P Q V Pvq

The Truth Table Represents Statements P Q And R Which Row Represent When P Q V P R Brainly Com

Mathematical Logic Part 2

Tangent Half Angle Formula Wikipedia
If 6 P 2 6 Q 5 And 6 R 15 What Is R In Terms Of P And Q Quora

P Q Derive To Pv Q Philosophy Stack Exchange

Find The Unit Vector In The Direction Of Pq Vector Where P And Q Are The Points 1 2 3 And 4 5 6 Youtube
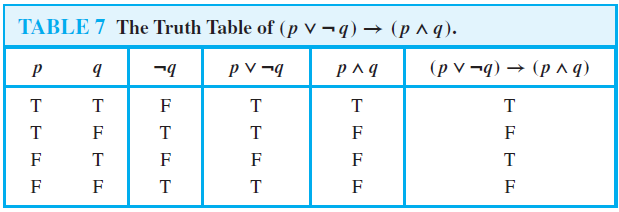
Truth Tables Of Compound Propositions
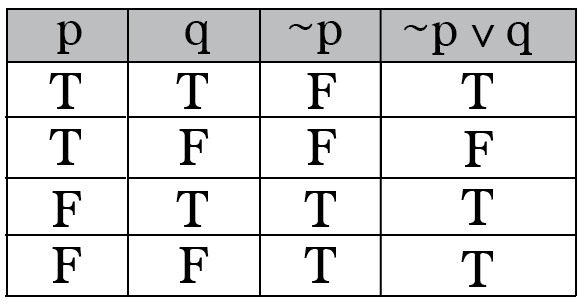
Intro To Truth Tables Boolean Algebra By Brett Berry Math Hacks Medium

Logic Explainability And The Future Of Understanding Stephen Wolfram Writings

Conditional Statements Easing The Hurry Syndrome

Logic Explainability And The Future Of Understanding Stephen Wolfram Writings
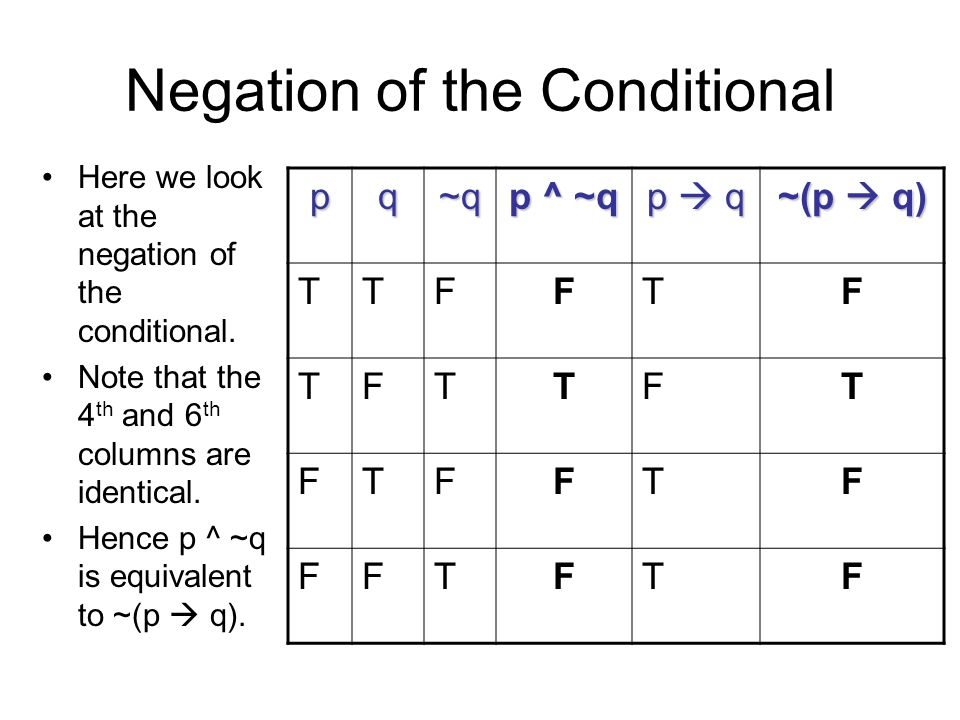
Truth Tables Section Ppt Video Online Download

Propositional Logic
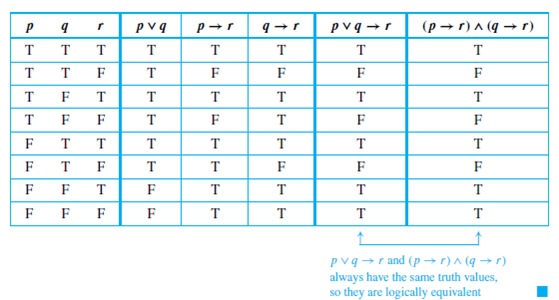
Solved Use The Logical Equivalence Established In Example To Chegg Com

How To Find The Negation Of P Q P Implies Q Math Application Of Derivatives Meritnation Com
9 If And Only If Using Theorems A Concise Introduction To Logic

How To Change Operator Symbols In Truth Table Tex Latex Stack Exchange
Http Eng Usf Edu Hady Courses Mgf1106 Documents Slides 3 3 Pdf
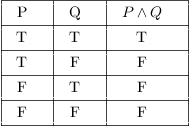
Truth Tables Tautologies And Logical Equivalences
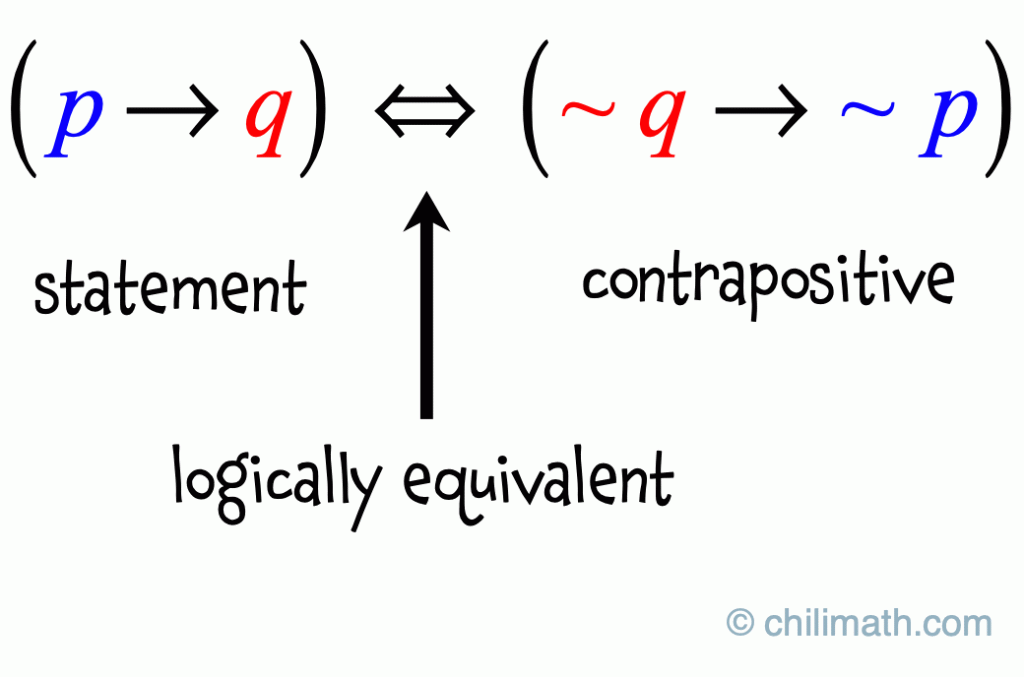
If N 2 Is Even Then N Is Even Chilimath
Propositional Logic Truth Table Boolean Algebra Dyclassroom Have Fun Learning

Ex 9 2 10 If Sum Of First P Terms Of Ap Is Equal To Ex 9 2

Truth Tables The Conditional And The Biconditional Implies And Iff Mathbootcamps

Logic And Proofs
Q Tbn 3aand9gctcyhof4gcdocwu6jlnli24t1p6nwxuwa4jtsdzykcgslzibwsm Usqp Cau

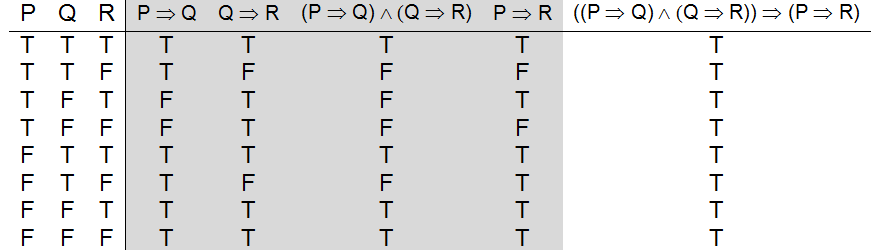
Let P Q R Denote Primitive Statements A Use Truth Tables To Verify The Following Logical Equivalences I Math Mathrm P Rightarrow Mathrm Q Wedge Mathrm R Leftrightarrow Mathrm P Rightarrow Mathrm Q Wedge Mathrm P Rightarrow

Quick Help Please The Truth Table Represents Statements P Q And R Which Statements Are True For Brainly Com

Ex 9 3 5 A Add P P Q Q Q R And R R P Ex 9 3

Lecture Notes In Discrete Mathematics
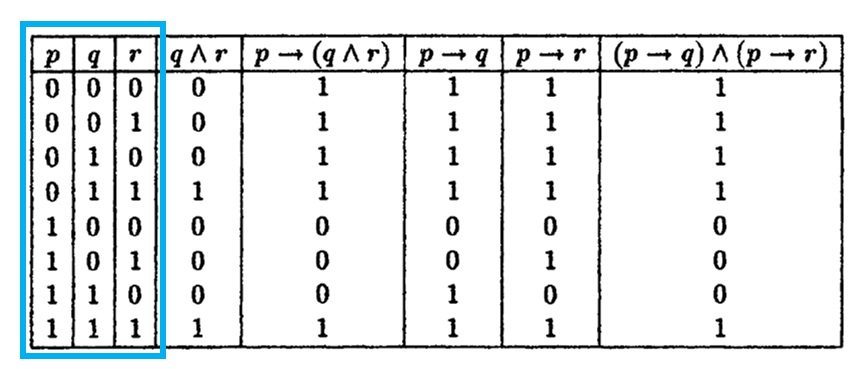
Let P Q R Denote Primitive Statements A Use Truth Tables To Verify The Following Logical Equivalences I Math Mathrm P Rightarrow Mathrm Q Wedge Mathrm R Leftrightarrow Mathrm P Rightarrow Mathrm Q Wedge Mathrm P Rightarrow

P Q Derive To Pv Q Philosophy Stack Exchange

Express 0 25 Bar In The Form Of P Q Brainly In
How To Solve P Q 4 P Q 4 8pq P 2 Q 2 Quora
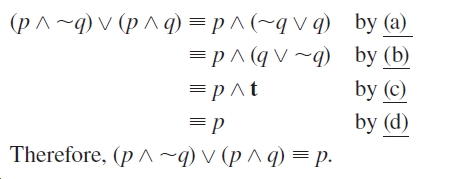
Answered Theorem 2 1 1 Logical Equivalences Bartleby
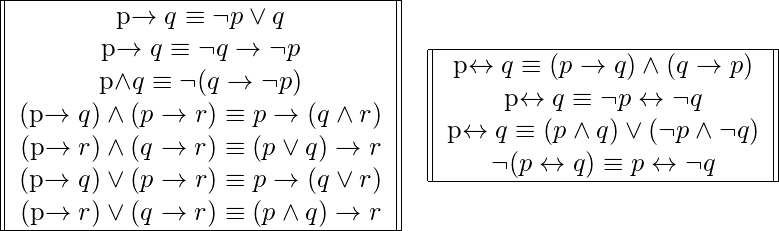
Mathematics Propositional Equivalences Geeksforgeeks

Solved Show That Q P P Q Is A Tautology I E Q Chegg Com

Logic Truth Table For P Q R Q Youtube

Module 1 Discrete Mathematics And Graph Theory
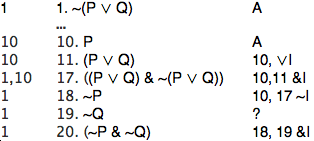
Sl15 Derivation Strategies
1

Truth Table

Show That Each Of These Conditional Statements Is A Tautology By Using Truth Tables A P P Q Q B P Q Q R P

The Logically Equivalent Proposition Of P Q Is

Ppt Logical Equivalence Powerpoint Presentation Free Download Id
Http Storm Cis Fordham Edu Zhang Cs2100 Slides Logic Handout Pdf

Solved For Each Of The Given Values Of N Pq And P 1 Chegg Com
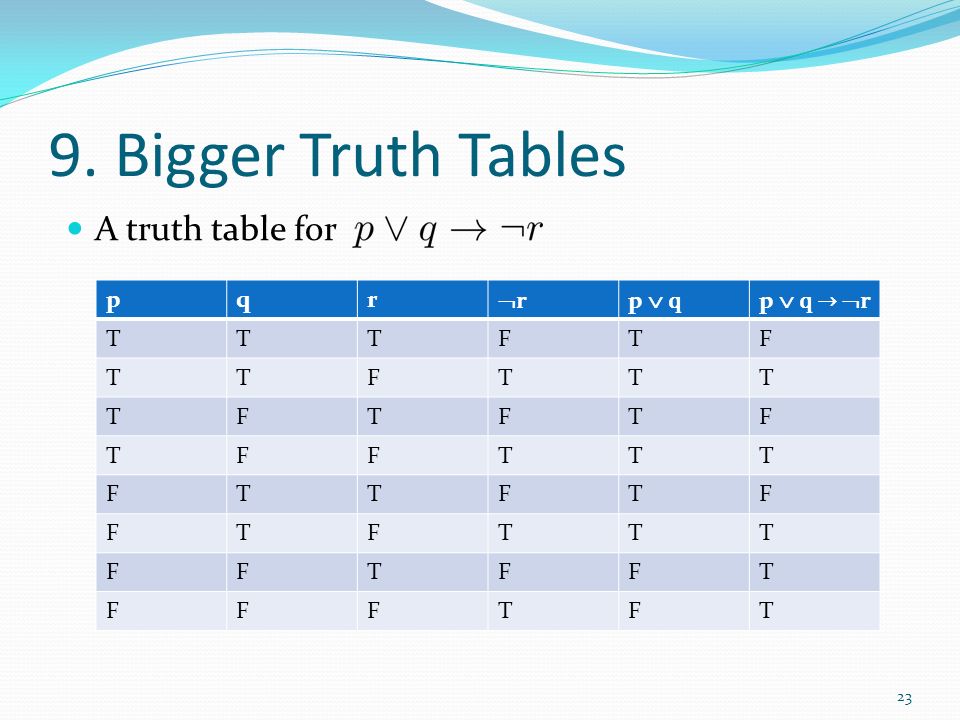
Discrete Maths 2 Propositional Logic Objective Ppt Video Online Download
If P Q Is The Sub Duplicate Ratio Of P X2 Q X2 What Is X2 Quora

Express The Following In The Form P Q Where P And Q Are Integers And Q 0 I 0 Bar6 Youtube
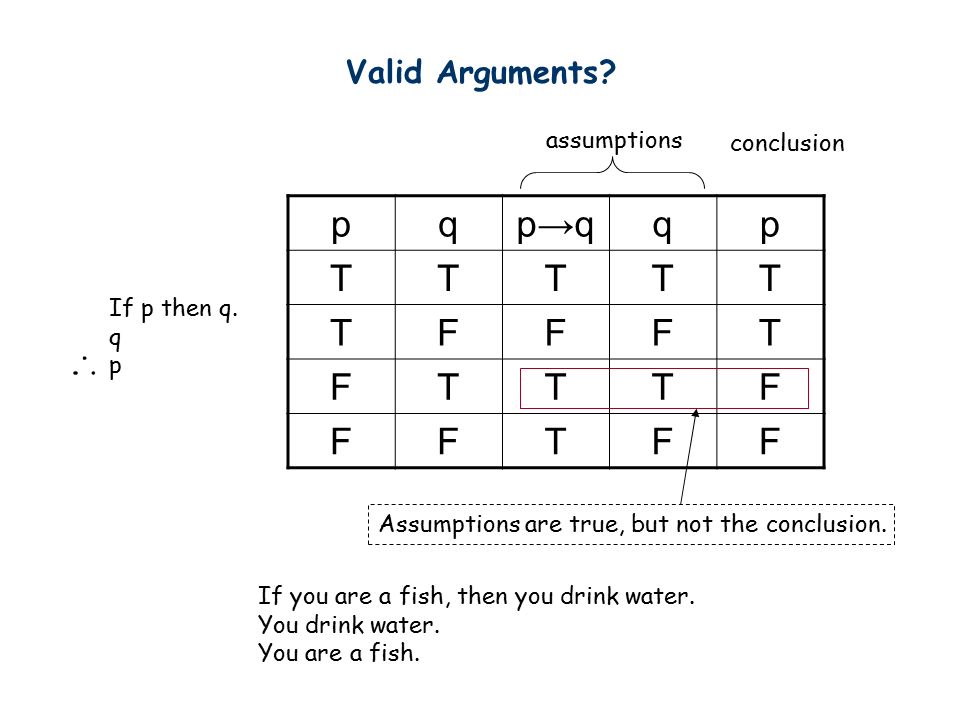
Propositional Logic Ppt Download

The Sheffer Stroke Internet Encyclopedia Of Philosophy
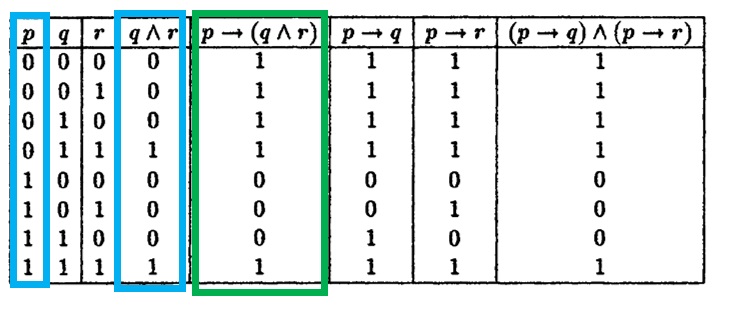
Let P Q R Denote Primitive Statements A Use Truth Tables To Verify The Following Logical Equivalences I Math Mathrm P Rightarrow Mathrm Q Wedge Mathrm R Leftrightarrow Mathrm P Rightarrow Mathrm Q Wedge Mathrm P Rightarrow

Solved Using The Thin Lens Equation A 1 F 1 P 1 Q W Chegg Com

Prepare The Truth Table Of The Following Exercise 1 5 Statement Patterns 1 P 9
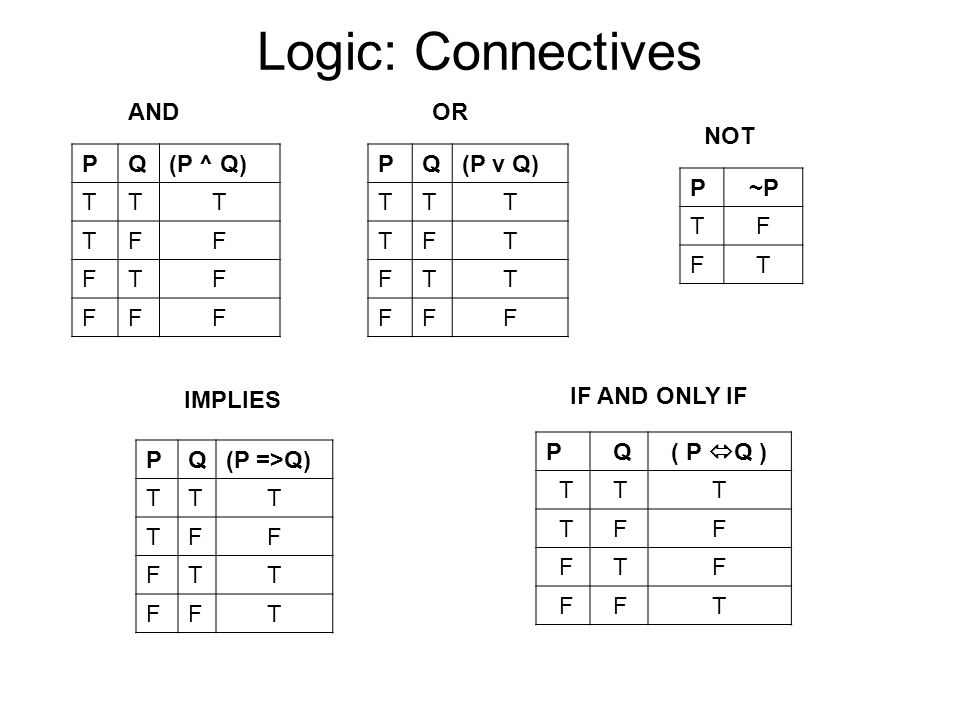
Logic Connectives And Or Not P Q P Q T F P Q P V Q T F P P T F Ppt Video Online Download

If P Q Are Prime Positive Integers Prove That Root P Root Q Is An Irrational Number Mathematics Topperlearning Com 044i7v44

Negating The Conditional If Then Statement P Implies Q Mathbootcamps
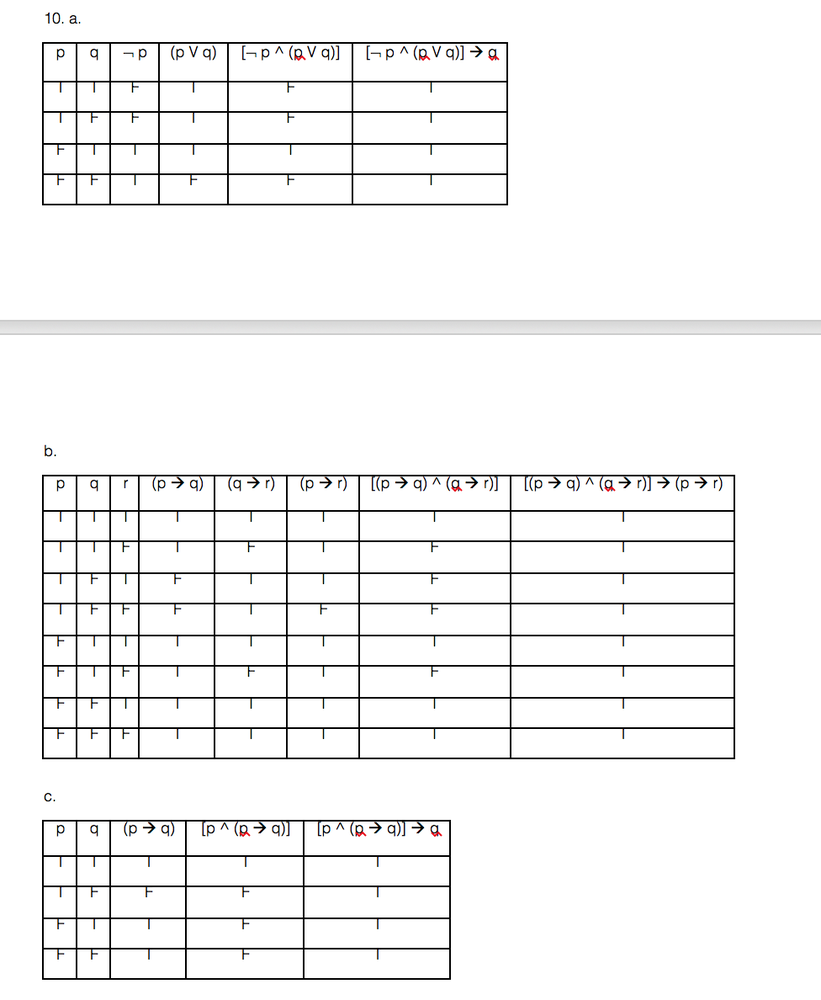
Show That Each Of These Conditional Statements Is A Tautology By Using Truth Tables A P P Q Q B P Q Q R P

Ssk3003 Discrete Structures Ppt Download
Mathematics Introduction To Propositional Logic Set 1 Geeksforgeeks
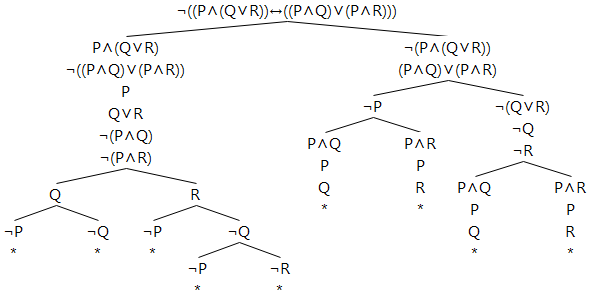
Inference And Replacement Rules

At What Angle Two Forces P Q And P Q Act So That Resultant Is

Negating The Conditional If Then Statement P Implies Q Mathbootcamps

Conditional Statements If P Then Q Youtube
Q Tbn 3aand9gcry3xjaajgsum6qh0wrmo Sl6jbxt Co7t7 Yvqzk15vqzjdg2 Usqp Cau

Centromere Position In P Arm Or Q Arm Of Chromosome



